Proses Produksi dan Biaya-Biaya

Dosen : Dr. Gerardus Herman Aswogumono MM., Dipl. SE

Tinjauan
I.  Analisis Produksi
Total Produk, Produk Marginal, Produk Rata-Rata
Isoquants
Isocost
Minimalisasi Biaya
II. Analisis Biaya
Biaya Total, Biaya Variabel, Biaya Tetap
Biaya Fungsi Kubik
Hubungan Biaya
III. Fungsi Biaya Multi-Produk

Analisis Produksi

• Fungsi Produksi
Q = F(K,L)
Jumlah output maksimal yang dapat diproduksi dengan K unit untuk modal dan L unit untuk tenaga kerja
• Keputusan Jangka Pendek vs. Keputusan Jangka Panjang
• Input Tetap vs. Input Variabel

Total Produk
• Fungsi produksi menurut Cobb-Douglas
• Contoh :
Q = F(K,L) = K0.5 L0.5
K adalah tetap sebanyak 16 unit
Fungsi produksi jangka pendek :
Q = (16)0.5 L0.5 = 4 L0.5
Produksi ketika 100 unit tenaga kerja digunakan :
Q = 4 (100)0.5 = 4(10) = 40 unit

Ukuran Produktivitas Marginal
• Produk Marginal Tenaga Kerja : MPL = ΔQ/ΔL
Mengukur output yang dihasilkan oleh pekerja terakhir
Kemiringan dari fungsi produksi jangka pendek (terhadap tenaga kerja)
• Produk Marginal Modal : MPK = ΔQ/ΔK
Mengukur output yang dihasilkan dari unit modal yang terakhir
Ketika modal dibiarkan berubah dalam jangka pendek maka MPK adalah kemiringan dari fungsi produksi (terhadap modal)

Ukuran Rata-Rata Produktivitas
• Produk Rata-Rata dari Tenaga Kerja
APL = Q/L
Mengukur output dari “rata-rata” pekerja
Contoh : Q = F(K,L) = K0.5 L0.5
Jika input adalah K = 16 dan L = 16, maka produk rata-rata dari tenaga kerja adalah APL = [(16)0.5(16)0.5]/16=1
• Produk Rata-Rata dari Modal
APK = Q/K
Mengukur output dari “rata-rata” unit modal
Contoh : Q = F(K,L) = K0.5L0.5
Jika input adalah K = 16 dan L = 16, maka produk rata-rata dari modal adalah APK = [(16)0.5(16)0.5]/16=1

Increasing, Diminishing and Negative Marginal Returns

Petunjuk untuk Proses Produksi
• Memproduksi dari fungsi produksi
Menyelaraskan insentif sebagai upaya untuk memaksimalkan usaha pekerja.
• Mempekerjakan pada input yang tepat
Ketika tenaga kerja atau modal berubah dalam jangka pendek, untuk memaksimalkan keuntungan seorang manajer akan mempekerjakan
Tenaga kerja sampai nilai dari produk marginal tenaga kerja sama dengan gaji :
VMPL = w, di mana VMPL = P x MPL
Modal sampai nilai produk marginal modal sama dengan tarif sewa :
VMPK = r, di mana VMPK = P x MPK

Isoquant

• Kombinasi dari input (K,L) yang memberi produsen tingkat output yang sama
• Bentuk dari isoquant mencerminkan kemudahan di mana produsen dapat mensubstitusi antara input-input sementara tetap menjaga tingkat output yang sama.

Marginal Rate of Technical Substitution (MRTS)

Marginal Rate of Technical Substitution (MRTS)

• Tingkat di mana dua input disubsitusikan dengan menjaga tingkat output yang sama

Isoquant Linear

Isoquant Linear

• Modal dan tenaga kerja adalah substitusi yang sempurna
Q = aK + bL
MRTSKL = b/a
Isoquant yang linear menyiratkan bahwa input-input dapat disubstitusi pada tingkat yang konstan, tidak terpengaruh dari tingkat input yang digunakan.

Leontief Isoquant

Leontief Isoquant

• Modal dan tenaga kerja adalah komplemen yang sempurna
• Modal dan tenaga kerja digunakan dalam proporsi yang tetap
• Q = min{bK,cL}
• Karena modal dan tenaga kerja digunakan dalam proporsi yang tetap maka tidak ada input pengganti sepanjang isoquant (sehingga, tidak ada MRTSKL)

Cobb-Douglas Isoquants

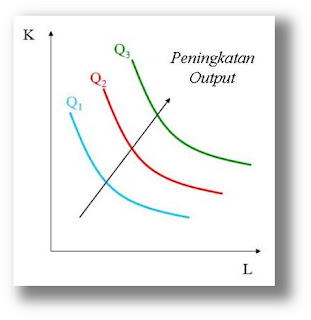Cobb-Douglas Isoquants

• Input tidak selamanya dapat disubstitusi
• Penurunan tingkat marginal dari teknis substitusi
 Ketika paling sedikit satu input digunakan dalam proses produksi, maka semakin bertambah banyak dari input yang lain yang harus digunakan untuk menghasilkan tingkat output yang sama.
• Q = KaLb
• MRTSKL = MPL/MPK

Isocost

Isocost

• Kombinasi dari input-input yang menghasilkan tingkat output pada biaya yang sama:
wL + rK = C
• Disusun kembali,
K = (l/r)C – (w/r)L
• Untuk harga input yang diberikan, isocost yang lebih jauh dari titik asal adalah berhubungan dengan biaya-biaya yang lebih tinggi
• Perubahan dari harga input mengubah kemiringan dari garis isocost

Minimalisasi Biaya

• Produk marginal per dollar yang dikeluarkan harus sama untuk semua input :

• Namun, hal ini hanya

Substitusi Input Optimal

• Sebuah perusahaan awalnya memproduksi Q0 dengan menggunakan kombinasi input yang diwakili oleh titik A pada biaya C0
• Misalkan w0 turun menjadi w1
  Kurva socost berputar berlawanan arah jarum jam; di mana mewakili tingkat biaya yang sama sebelum perubahan gaji.
  Untuk menghasilkan tingkat output yang sama, Q0, perusahaan akan menghasilkan isocost pada garis yang lebih rendah (C1) pada titik B
  Kemiringan dari garis isocost yang baru mewakili hubungan gaji yang lebih rendah terhadap tarif sewa modal

Analisis Biaya

• Jenis-jenis Biaya
Biaya Tetap / Fixed Cost (FC)
Biaya Variabel / Variable Cost (VC)
Biaya Total / Total Cost (TC)
Biaya Penyusutan / Sunk Cost

Biaya Total dan Biaya Variabel

Biaya Total dan Biaya Variabel

C(Q) : Biaya total minimum untuk menghasilkan berbagai tigkat alternatif output

C(Q) = VC(Q) + FC

VC(Q) :  Biaya yang berbeda dengan output

FC : Biaya yang tidak      berbeda dengan output

Biaya Tetap dan Biaya Penyusutan

Biaya Tetap dan Biaya Penyusutan

FC : Biaya yang tidak berubah  karena perubahan output

Biaya Penyusutan :
Biaya yang selamanya hilang setelah dibayarkan

Beberapa Definisi

Beberapa Definisi

Average Total Cost
ATC = AVC + AFC
ATC = C(Q)/Q
Average Variable Cost
AVC = VC(Q)/Q
Average Fixed Cost
AFC = FC/Q
Marginal Cost
MC = ΔC/ΔQ

Biaya Tetap (Fixed Cost)

Biaya Variabel (Variable Cost)

Biaya Total (Total Cost)

Fungsi Kubik Biaya

• C(Q) = f + aQ + bQ2 + cQ3
• Biaya Marginal?
Dihafalkan :
MC(Q) = a + 2bQ + 3cQ2
Kalkulus :
dC/dQ = a + 2bQ + 3cQ2

Contoh
• Biaya Total : C(Q) = 10 + Q + Q2
• Fungsi biaya variabel : VC(Q) = Q + Q2
• Biaya variabel untuk memproduksi 2 unit :
VC(2) = 2 + (2)2 = 6
• Biaya tetap : FC = 10
• Fungsi biaya marginal : MC(Q) = 1 + 2Q
• Biaya marginal untuk memproduksi 2 unit :
MC(2) = 1 + 2(2) = 5

Skala Ekonomi

Fungsi Biaya Multi-Produk

• C(Q1,Q2) : Biaya untuk menghasilkan dua output secara bersama
• Bentuk umum fungsi :
C(Q1,Q2) = f + aQ1Q2 + bQ12 + cQ22

Lingkup Ekonomi
• C(Q1,0) + C(0,Q2) > C(Q1,Q2)
Adalah lebih murah untuk menghasilkan dua output secara bersama-sama daripada secara terpisah
• Contoh :
 Adalah lebih murah bagi Time-Warner untuk memproduksi layanan koneksi internet dan layanan Instant Messaging secara bersama-sama daripada secara terpisah

Komplementaritas Biaya
• Biaya marginal dari produksi barang 1 menurun karena banyak dari barang 2 diproduksi :
ΔMC1(Q1,Q2)/ΔQ2 < 0

• Contoh :
Sapi bersembunyi dan menyerang

Fungsi Kuadrat Biaya Multi-Produk

• C(Q1,Q2) = f + aQ1Q2 + (Q1)2 + (Q2)2
• MC1(Q1,Q2) = aQ2 + 2Q1
• MC2(Q1,Q2) = aQ1 + 2Q2
• Komplementaritas biaya :  a < 0
• Lingkup ekonomi : f > aQ1Q2
C(Q1,0) + C(0,Q2) = f + (Q1)2 + f + (Q2)2
C(Q1,Q2) = f + aQ1Q2 + (Q1)2 + (Q2)2
f > aQ1Q2 : Produksi bersama lebih murah

Contoh Numerik :
• C(Q1,Q2) = 90 - 2Q1Q2 + (Q1)2 + (Q2)2
• Komplementaritas biaya?
Ya, ketika a = -2 < 0
MC1(Q1,Q2) = -2Q2 + 2Q1
• Lingkup Ekonomi?
Ya, ketika 90 > -2Q1Q2

Kesimpulan

• Untuk memaksimalkan keuntungan (meminimalkan biaya) manajer harus menggunakan input sedemikian rupa sehingga nilai marginal dari tiap input mencerminkan harga yang harus dibayar perusahaan untuk menggunakan input
• Input optimal dapat dicapai ketika 
• MRTSKL = (w/r)
• Fungsi biaya merupakan dasar untuk membantu menentukan perilaku memaksimalkan keuntungan di bab selanjutnya.