Dosen : Dr. Gerardus Herman Aswogumono MM., Dipl. SE
Jika EG,S > 0, maka S dan G hubungan langsung
Jika EG,S < 0, maka S dan G hubungan terbalik
Jika EG,S = 0, maka S dan G tidak berhubungan
Menggunakan Kalkulus
Sebuah jalan alternatif untuk menghitung elastisitas sebuah fungsi G=f(S) adalah
Jika EG,S > 0, maka S dan G hubungan langsung
Jika EG,S < 0, maka S dan G hubungan terbalik
Jika EG,S = 0, maka S dan G tidak berhubungan
• Tanda negatif menunjukkan “hukum permintaan”
Elastic : |EQx,Px | > 1
Inelastic : |EQx,Px | < 1
Unitary : |EQx,Px | = 1
Elastisitas Harga Sendiri dan Total Pendapatan
• Elastic
Kenaikan (penurunan) harga menyebabkan sebuah penurunan (kenaikan) dalam total pendapatan
• Inelastic
Kenaikan (penurunan) harga menyebabkan sebuah kenaikan (penurunan) dalam total pendapatan
• Unitary
Total pendapatan adalah maksimal pada titik di mana permintaan adalah unitary elastic
Semakin banyak barang substitusi, permintaan semakin elastis
• Waktu
Permintaan cenderung semakin inelastis dalam jangka pendek daripada dalam jangka panjang
Waktu memberikan ruang yang lebih dalam membantu konsumen mencari barang substitusi
• Bagian Pengeluaran
Barang yang dibeli dari sebagian kecil anggaran konsumen cenderung lebih inelastis daripada barang yang dibeli dari sebagian besar penghasilan mereka.
Prediksi Perubahan Pendapatan dari Dua Produk
• Anggap perusahaan menjual barang yang saling berkaitan. Jika harga x berubah maka total pendapatan akan berubah menjadi :
• Jika EQx,M > 0, maka x adalah barang normal
• Jika EQx,M < 0, maka x adalah barang inferior
Kegunaan Elastisitas
• Penentuan harga
• Mengelola aliran dana
• Berpengaruh pada perubahan harga pesaing
• Berpengaruh pada kecenderungan dan resesi ekonomi
• Berpengaruh pada kampanye iklan
• Dan lain-lain
Contoh 1 :
Penentuan Harga dan Aliran Dana
Contoh 2:
Mengukur Perubahan
Jawab
Contoh 3 :
Dampak dari Perubahan dalam Harga Pesaing
Jawab
• Contoh :
• X dan Y adalah subsitusi (koefisien dari PY adalah positif )
• X adalah barang inferior (koefisien dari M adalah negatif)
Contoh Permintaan Linear
• Qd = 10 - 2P
• Elastisitas Harga Sendiri : (-2)P/Q
• Jika P=1, Q=8 (karena 10 – 2 = 8)
• Elastisitas harga barang sendiri ketika
P=1, Q=8 :
(-2)(1)/8 = - 0.25
Permintaan Log-Linear
• Fungsi Umum Permintaan Log-Linear :
Elastisitas harga sendiri : βX
Elastisitas harga silang : βY
Elastisitas penghasilan : βM
Contoh Permintaan Log-Linear
• Pengertian dan konsep penting :
Least Square Regression : Y = a + bX + e
Confidence Intervals
t-statistic
R-square or Coefficient of Determination
F-statistic
Contoh
• Gunakan lembar kerja untuk mengestimasi fungsi permintaan log-linear berikut ini
ln Qx= β0 + βx lnPx + e
ln(Qx) = 7.58 – 0.84 ln(Px)
Elastisitas harga sendiri : -0.84 (inelastis)
• Seberapa baguskah estimasi kita?
t-statistik dari 5.29 dan -2.80 menunjukkan bahwa koefisien estimasi adalah secara statistik tidak sama dengan nol
R-square dari 0.17 menunjukkan bahwa model ini menjelaskan hanya 17 persen dari variasi dalam ln(Qx)
F-statistic signifikan pada level 1 persen
• Memberikan pasar atau survei data, analisis regresi dapat digunakan untuk mengestimasi :
Fungsi permintaan
Elastisitas
Dan banyak hal lain, termasuk fungsi biaya
• Manajer dapat menghitung pengaruh perubahan dalam harga, penghasilan, periklanan, dll.
Konsep Elastisitas
Bagaimana pengaruh variabel “G” untuk merubah dalam variabel “S” |
| Konsep Elastisitas |
Jika EG,S > 0, maka S dan G hubungan langsung
Jika EG,S < 0, maka S dan G hubungan terbalik
Jika EG,S = 0, maka S dan G tidak berhubungan
Menggunakan Kalkulus
Sebuah jalan alternatif untuk menghitung elastisitas sebuah fungsi G=f(S) adalah
 |
| Menggunakan Kalkulus |
Jika EG,S < 0, maka S dan G hubungan terbalik
Jika EG,S = 0, maka S dan G tidak berhubungan
Elastisitas Harga Barang dalam Permintaan
 |
| Elastisitas Harga Barang dalam Permintaan |
• Tanda negatif menunjukkan “hukum permintaan”
Elastic : |EQx,Px | > 1
Inelastic : |EQx,Px | < 1
Unitary : |EQx,Px | = 1
 |
| Elastis Sempurna & Permintaan Tidak Elastis |
Elastisitas Harga Sendiri dan Total Pendapatan
• Elastic
Kenaikan (penurunan) harga menyebabkan sebuah penurunan (kenaikan) dalam total pendapatan
• Inelastic
Kenaikan (penurunan) harga menyebabkan sebuah kenaikan (penurunan) dalam total pendapatan
• Unitary
Total pendapatan adalah maksimal pada titik di mana permintaan adalah unitary elastic
 |
| Elastisitas, Total Pendapatan dan Permintaan Linear |
Faktor-faktor yg mempengaruhi Elastisitas Harga Sendiri
• Ketersediaan Barang SubstitusiSemakin banyak barang substitusi, permintaan semakin elastis
• Waktu
Permintaan cenderung semakin inelastis dalam jangka pendek daripada dalam jangka panjang
Waktu memberikan ruang yang lebih dalam membantu konsumen mencari barang substitusi
• Bagian Pengeluaran
Barang yang dibeli dari sebagian kecil anggaran konsumen cenderung lebih inelastis daripada barang yang dibeli dari sebagian besar penghasilan mereka.
Elastisitas Harga Silang dari Permintaan
 |
| Elastisitas Harga Silang dari Permintaan |
• Anggap perusahaan menjual barang yang saling berkaitan. Jika harga x berubah maka total pendapatan akan berubah menjadi :
 |
| Prediksi Perubahan Pendapatan dari Dua Produk |
 |
| Elastisitas Penghasilan |
• Jika EQx,M > 0, maka x adalah barang normal
• Jika EQx,M < 0, maka x adalah barang inferior
Kegunaan Elastisitas
• Penentuan harga
• Mengelola aliran dana
• Berpengaruh pada perubahan harga pesaing
• Berpengaruh pada kecenderungan dan resesi ekonomi
• Berpengaruh pada kampanye iklan
• Dan lain-lain
Contoh 1 :
Penentuan Harga dan Aliran Dana
- Berdasarkan pada laporan FTC oleh Michael Ward, elastisitas harga sendiri AT&T dari permintaan untuk pelayanan jangka panjang adalah sebesar -8.64
- AT&T membutuhkan peningkatan pendapatan dalam rangka untuk mencapai tujuan pemasaran
- Untuk mencapai tujuan tersebut maka seharusnya AT&T menaikkan atau menurunkan harga?
- Karena permintaan adalah elastis, penurunan harga akan meningkatkan kuantitas permintaan dengan prosentase lebih besar daripada penurunan harga, maka akan meningkatkan pendapatan bagi AT&T
Contoh 2:
Mengukur Perubahan
- Jika AT&T menurunkan harga hingga 3 persen, apa yang akan terjadi pada panggilan telepon jarak jauh melalui AT&T?
Jawab
- Panggilan akan naik 25.92 persen!
Contoh 3 :
Dampak dari Perubahan dalam Harga Pesaing
- Berdasarkan pada laporan FTC oleh Michael Ward, harga elastisitas silang AT&T dari permintaan untuk layanan jangka panjang adalah 9.06
- Jika pesaing menurunkan harga mereka sebesar 4 persen, apa yang akan terjadi pada permintaan untuk layanan AT&T?
Jawab
- Permintaan AT&T akan jatuh 36.24 persen!
Interpretasi Fungsi Permintaan
• Penyajian secara matematis dari kurva permintaan• Contoh :
 |
| Interpretasi Fungsi Permintaan |
• X dan Y adalah subsitusi (koefisien dari PY adalah positif )
• X adalah barang inferior (koefisien dari M adalah negatif)
Fungsi Permintaan Linear
• Fungsi Permintaan Linear secara umum : |
| Fungsi Permintaan Linear |
Contoh Permintaan Linear
• Qd = 10 - 2P
• Elastisitas Harga Sendiri : (-2)P/Q
• Jika P=1, Q=8 (karena 10 – 2 = 8)
• Elastisitas harga barang sendiri ketika
P=1, Q=8 :
(-2)(1)/8 = - 0.25
Permintaan Log-Linear
• Fungsi Umum Permintaan Log-Linear :
 |
| Permintaan Log-Linear |
Elastisitas harga sendiri : βX
Elastisitas harga silang : βY
Elastisitas penghasilan : βM
Contoh Permintaan Log-Linear
- ln(Qd) = 10 – 2 ln(P)
- Elastisitas harga sendiri : -2
 |
| Penyajian Grafis dari Permintaan Linear dan Log-Linear |
Analisis Regresi
• Salah satu kegunaan untuk mengestimasi fungsi permintaan• Pengertian dan konsep penting :
Least Square Regression : Y = a + bX + e
Confidence Intervals
t-statistic
R-square or Coefficient of Determination
F-statistic
Contoh
• Gunakan lembar kerja untuk mengestimasi fungsi permintaan log-linear berikut ini
ln Qx= β0 + βx lnPx + e
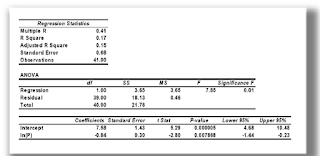 |
| Summary Output |
Interprestasi Output Regresi
• Estimasi fungsi permintaan log-linear :ln(Qx) = 7.58 – 0.84 ln(Px)
Elastisitas harga sendiri : -0.84 (inelastis)
• Seberapa baguskah estimasi kita?
t-statistik dari 5.29 dan -2.80 menunjukkan bahwa koefisien estimasi adalah secara statistik tidak sama dengan nol
R-square dari 0.17 menunjukkan bahwa model ini menjelaskan hanya 17 persen dari variasi dalam ln(Qx)
F-statistic signifikan pada level 1 persen
Kesimpulan
• Elastisitas adalah alat yang bisa anda gunakan untuk menghitung pengaruh perubahan harga, penghasilan, iklan penjualan, dan pendapatan• Memberikan pasar atau survei data, analisis regresi dapat digunakan untuk mengestimasi :
Fungsi permintaan
Elastisitas
Dan banyak hal lain, termasuk fungsi biaya
• Manajer dapat menghitung pengaruh perubahan dalam harga, penghasilan, periklanan, dll.









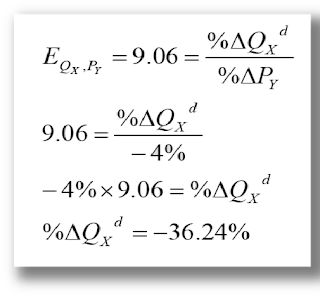
Posting Komentar
Berkomentar sesuai dengan judul blog ini yah, berbagi ilmu, berbagi kebaikan, kunjungi juga otoriv tempat jual aksesoris motor dan mobil lengkap